基本再生産数（きほんさいせいさんすう、英語: basic reproduction number、R0と表記され、R noughtあるいはR zeroと読まれる）とは、疫学において、感染症に感染した1人の感染者が、誰も免疫を持たない集団に加わったとき、直接感染させる人数の期待値である。1人の患者が平均して何人に感染を広げる可能性があるかを示す。
また、人口学においては女性が生涯に生む期待女児数（純再生産率）を指す。女性が1人だけ娘を産むときには人口は単純再生産であって、1人より多く産めば拡大再生産となる。すなわち母親世代とその娘世代の総数比を指し、R0 が1より大きければ人口は拡大再生産されるが、1より小さければ縮小再生産される。
基本再生産数は、人口学で生まれた概念であるが、感染症疫学でも基本概念である。R0 は、人口学では人口増加の閾値として用いられ、進化生物学においては侵入生物ないし突然変異体の適応度と解釈され、感染症疫学では感染症の侵入条件や臨界免疫化割合を定量化するものと見なされる。
疫学
定義
すべての個体が感染症に対する感受性をもつ集団内で、一感染個体により直接生み出される感染個体数の平均と考えられる。この定義は他の個体はすべて感染しておらず、（先天性の、あるいはワクチン接種による）免疫をもっていない状況を記述している。オーストラリア保健省による定義などでは「感染症の伝播に対する計画的な介入」のないことが付け加えられてる。
定義により基本再生産数 R0 はワクチン接種により変更することはできない。また基本再生産数 R0 は無次元数であり、倍加時間 のような時間の単位 をもつ割合ではないことに注意が必要である。
基本再生産数 R0 は、環境因子や感染集団の行動による影響も受けるため、病原体に対する生物学的な定数ではない。さらに、基本再生産数 R0 の値は通常、数理モデルから推定されるので、推定値は使用されたモデルや他のパラメータの値に依存する。したがって、文献における値は特定の文脈においてのみ意味があり、古い値を使用したり、異なるモデルに基づく値を比較したりするべきではない。また基本再生産数 R0 自体は集団内における感染症の蔓延する速度を推定するものではない。
感染症モデル
基本再生産数 R0 の最も重要な用途は新興感染症が集団内に蔓延するかどうかを決定することと、感染症を撲滅するためには集団のどのくらいの割合にワクチン接種をして免疫化すべきなのかを決定することである。一般に使用される感染症モデルでは R0 > 1 のとき、感染症は集団内で蔓延をはじめ、R0 < 1 のときには蔓延しない。一般的に基本再生産数 R0 の値が大きいほど、流行を抑制するのは難しい。単純なモデルでは、感染症の持続的な蔓延を防ぐためには、実質的に免疫化される（＝感受性のない）べき集団の割合は集団免疫閾値
- 1 − 1/R0
を超えなくてはならない；一方でエンデミックな定常状態における感受性個体数の割合は 1/R0 である。
基本再生産数は、感染個体の感染力の持続時間・微生物の感染性・感染個体が接触している集団における感受性個体数を含むいくつもの要因による影響を受ける。
疫学上、感染症流行を予測・抑制することは公衆衛生上で重要な課題であり、その問題に対して、個体群生態学で使用された数理モデルの安定性分析などが感染症疫学でも流用できたことから、この研究分野が発展する事となった。
感染個体が単位時間あたり平均 β の感染を生み出す接触をし、感染性期間が平均 τ であると仮定する。このとき基本再生産数は
- R0 = βτ
で与えられる。この単純な式は R0 を減らし、最終的には感染の伝播を減らすいくつかの方法を示唆する。単位時間あたりの接触を減らす（たとえば、伝播が他者との接触を必要とする場合には、家に留まる）、または（防護具などによって）感染を生み出す接触の割合を減らすことで、単位時間あたりの感染を生み出す接触の平均 β を減らすことができる。また感染個体をできるだけ早く発見し、隔離／治療／殺処分（動物の場合によくある）することで、感染性期間の平均 τ を減らすことができる。
区画モデル
疫学における区画モデルの代表例としてSIRモデルがある。SIRモデルは感受性 (Susceptible)、感染した (Infected)、隔離された（Removed: 回復または死亡）人の個体数の経時的な疾患動態を説明する。なお、SIRモデルの R(0)と基本再生産数の R0 を混同しないように注意。前者は t = 0 での隔離者数を表わす。
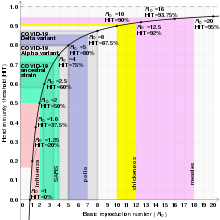
感染症の基本再生産数値
| 感染症 | 伝染 | R0 | 集団免疫のしきい値 |
|---|---|---|---|
| 麻疹（はしか） | エアロゾル | 12–18 | 92–94% |
| 水痘（水ぼうそう） | エアロゾル | 10–12 | 90–92% |
| 流行性耳下腺炎（おたふく風邪） | 呼吸器飛沫 | 10–12 | 90–92% |
| COVID-19（デルタ株） | 呼吸器飛沫とエアロゾル | （5-9.5） | 80–89% |
| 風疹 | 呼吸器飛沫 | 6–7 | 83–86% |
| ポリオ | 糞口経路 | 5–7 | 80–86% |
| 百日咳 | 呼吸器飛沫 | 5.5 | 82% |
| 天然痘 | 呼吸器飛沫 | 3.5–6.0 | 71–83% |
| COVID-19（アルファ株） | 呼吸器飛沫とエアロゾル | 4–5 | 75–80% |
| HIV/AIDS | 体液 | 2–5 | 50–80% |
| COVID-19（野生型） | 呼吸器飛沫とエアロゾル | 2.9 (2.4–3.4) | 65% (58–70%) |
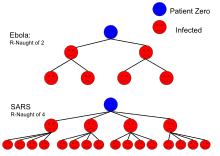
| SARS | 呼吸器飛沫 | 2–4 | 50–75% |
| ジフテリア | 唾液 | 2.6 (1.7–4.3) | 62% (41–77%) |
| インフルエンザ（スペインかぜ） | 呼吸器飛沫 | 2–3 | 50–67% |
| 風邪 | 呼吸器飛沫 | 2–3 | 50–67% |
| エボラ（2014年のエボラ出血熱の流行） | 体液 | 1.8 (1.4–1.8) | 44% (31–44%) |
| インフルエンザ（2009年のパンデミック株） | 呼吸器飛沫 | 1.6 (1.3–2.0) | 37% (25–51%) |
| インフルエンザ （季節株） | 呼吸器飛沫 | 1.3 (1.2–1.4) | 23% (17–29%) |
| ニパウイルス | 体液 | 0.48 | 0% |
| MERS | 呼吸器飛沫 | 0.47 (0.29–0.80) | 0% |
限界
数理モデル、特に微分方程式から計算をするとき、R0 であると言われる数の多くは、実際には単なる閾値であって、2次感染者数の平均ではない。そのような閾値を数理モデルから導出する多くの手法があるが、常に R0 の真値を与えるものはほとんどない。これはマラリアのように宿主間に媒介動物がいる場合は特に問題が多い。
これらの閾値は疾病が絶滅（R0 < 1）するか流行（R0 > 1）するかを決定するが、一般にそれらを異なる疾病で比較することはできない。したがって、上の表にある値は慎重に用いる必要がある。（特に数理モデルから計算された場合。）
手法には生存関数・ヤコビ行列の最大固有値の再配置・next-generation method・内的自然増加率からの計算・エンデミックな定常状態の感受性人口からの計算・平均感染年齢からの計算・最終規模方程式からの計算などがある。多くの手法は、たとえ同じ微分方程式から出発したとしても、互いに一致しない。実際に2次感染者の平均を計算しているものはさらに少ない。基本再生産数 R0 が実地で観測されることは滅多になく、通常は数理モデルから計算され、これにより有用性は著しく制限される。
実効再生産数
基本再生産数を、実効再生産数 R と混同してはならない。実効再生産数とは、感染個体がすでに存在するかもしれない現在の集団内で、一感染個体により直接生み出される感染個体数の平均である。
広東省疾病予防コントロールセンターによれば、「伝染性を表現するために実効再生産数 (R) がより一般的に使用される。実効再生産数は感染症例ごとによって発生する二次症例数の平均として定義される。管理措置がない場合、R = R0 χ (χは感受人口の割合) となる。」。例えば2019-nCoVの実効再生産数は2.9で、SARSの実効再生産数は1.7となる。
人口学
人口学において、基本再生産数 R0 は、1人の女性が生まれてから a 歳まで生き延びる確率（生残率）l(a) と、年齢ごとの年齢別女児出生率 β(a) の積を総和した数字
である。約2.08倍すると男女込みの平均出生児数または、少子化の資料に頻出する合計特殊出生率（TFR）となる。
基本再生産数は、母親世代とその娘世代の総数比を指し、R0 が1より大きければ人口は拡大再生産されるが、1より小さければ縮小再生産される。長期的にみれば、R0 > 1であれば人口は増加し、R0 < 1 であれば人口減少がおきる。
日本人口の2005年の R0 は0.61で、これは母親世代の人口の6割程の数の娘しか生まれてこないことを意味する。
学説史
人口のレベルで感染症がどのように広がっていくのか、また制御するための介入についての数理モデルを使った研究は、18世紀のスイスの数学者ダニエル・ベルヌーイの天然痘死亡率が人間の寿命に与える影響研究に遡り、これは区画モデルの端緒だった。天然痘による死亡リスクというものがなくなった場合に寿命はどう延びるか、つまり、いくつかの競合する死因がある場合に、そのうちの一つが取り除かれたら寿命がどの程度延びるか、という競合リスクモデルの研究の端緒となった。
ダニエル・ベルヌーイは1766年にフランス王立科学アカデミーで天然痘罹患率と死亡率データ分析「小虫を死因とした死亡例の新解析（Essai d’une nouvelle analyse de la mortalite causee par la petite verole）」を発表した。これは予防接種の効果計測や、観察の打ち切り（センサリング censoring） などの知見を含めた最初期の統計学上の解析となった。
脚注
注釈
参考文献
- 稲葉寿「感染症の数理」東京大学大学院数理科学研究科平成 20 年度年第 7 回例会「医療とアクチュアリー」講演 2009年3月18日
- 稲葉寿,「基本再生産数 R0 の数学 (PDF) 」『日本数理生物学会ニュースレターJSMB Newsletter』 No. 64, pp. 1–7, 2011年
- 稲葉寿, 「基本再生産数理論の最近の進歩 (第10回生物数学の理論とその応用)」『数理解析研究所講究録』 1917巻 p. 143–152、2014年, 京都大学数理解析研究所, ISSN 1880-2818
- 稲葉寿,「基本再生産数 R0 の数理(<特集>感染症の数理モデルと制御)」『システム/制御/情報』 59巻 12号 p. 434-439, 2015年、doi:10.11509/isciesci.59.12_434
- 西浦博; 稲葉寿 (2006), “感染症流行の予測：感染症数理モデルにおける定量的課題（特集 予測と発見）”, 統計数理 (統計数理研究所) 54 (2): 461–480
- 日本環境感染学会 (2018), 用語集・用語解説集（第4版）
- Jones, James Holland. “Notes on R0”. 2018年11月6日閲覧。
- Liu, Tao; Hu, Jianxiong; Kang, Min; Lin, Lifeng; Zhong, Haojie; Xiao, Jianpeng; He, Guanhao; Song, Tie et al. (2020-01-25). “Transmission dynamics of 2019 novel coronavirus (2019-nCoV)” (英語). bioRxiv: 2020.01.25.919787. doi:10.1101/2020.01.25.919787.